LTM(Local Transformation Module)[1] focus on the relationship of the local features. It uses linear transformation of the relationship matrix in a high-dimensional metric embedding space to accomplish the transformation. There are some details of reading and implementing it.

Contents

• Paper & Code & note
• Paper understanding
• Code understanding
• Note
• References

Paper & Code & note

Paper: A New Local Transformation Module for Few-Shot Segmentation(ICMM 2020 paper)
Code: [Code]
Note: Mendeley

Paper

Abstract

1. The key step of few-shot segmentation is to establish the transformation module.
2. The existing methods form transformation model based on global cues, which however ignores the local cues.
3. This paper proposes a new transformation module based on local cues,
   relationship matrix with cosine distance to enhance the generalization, generalized inverse matrix to handle the challenging mapping problem.
4. It outperforms the state-of-the-art method on the PASCAL VOC 2012 dataset.

Problem Description

Problem Solution

Conceptual Understanding

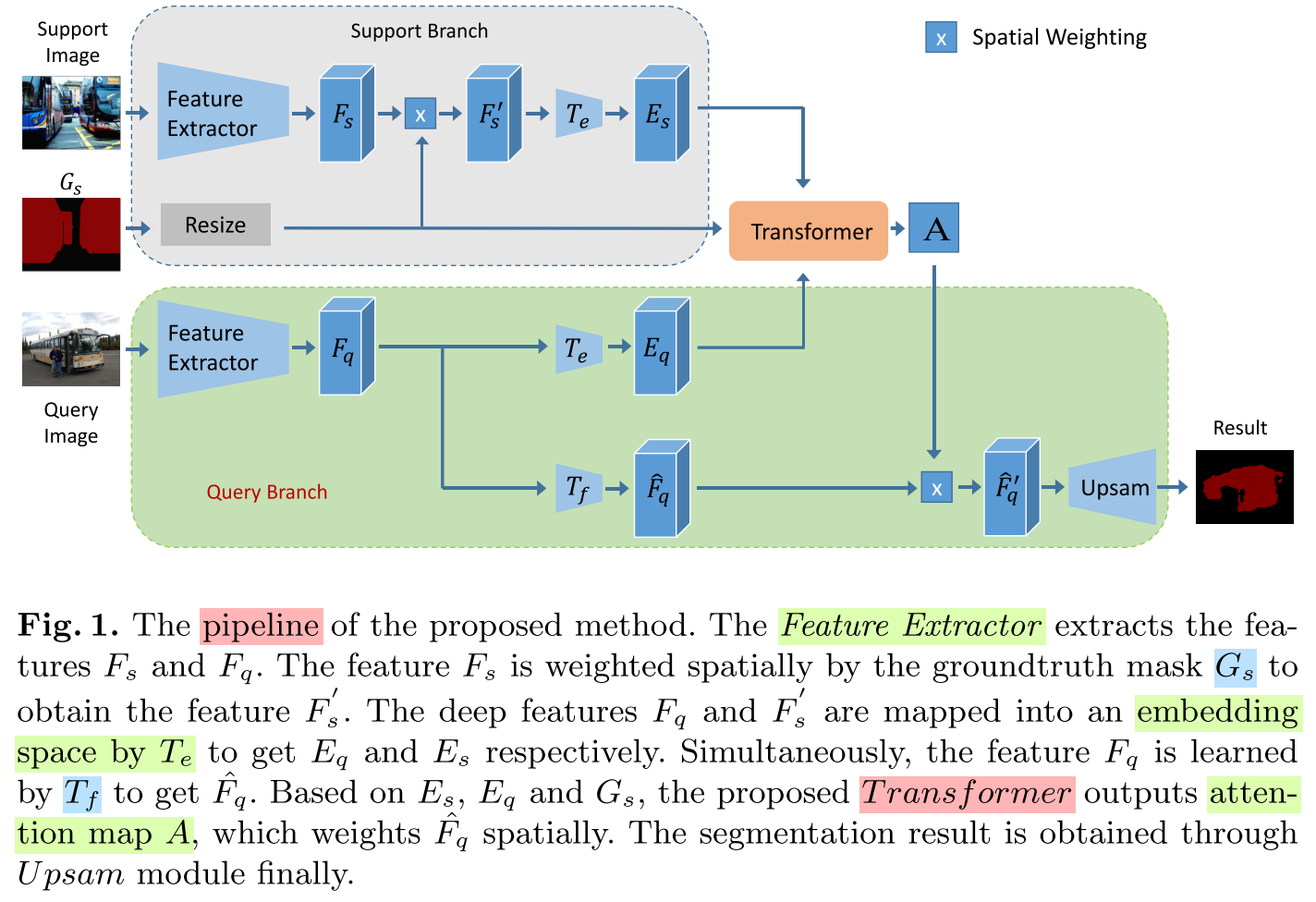
Core Conception

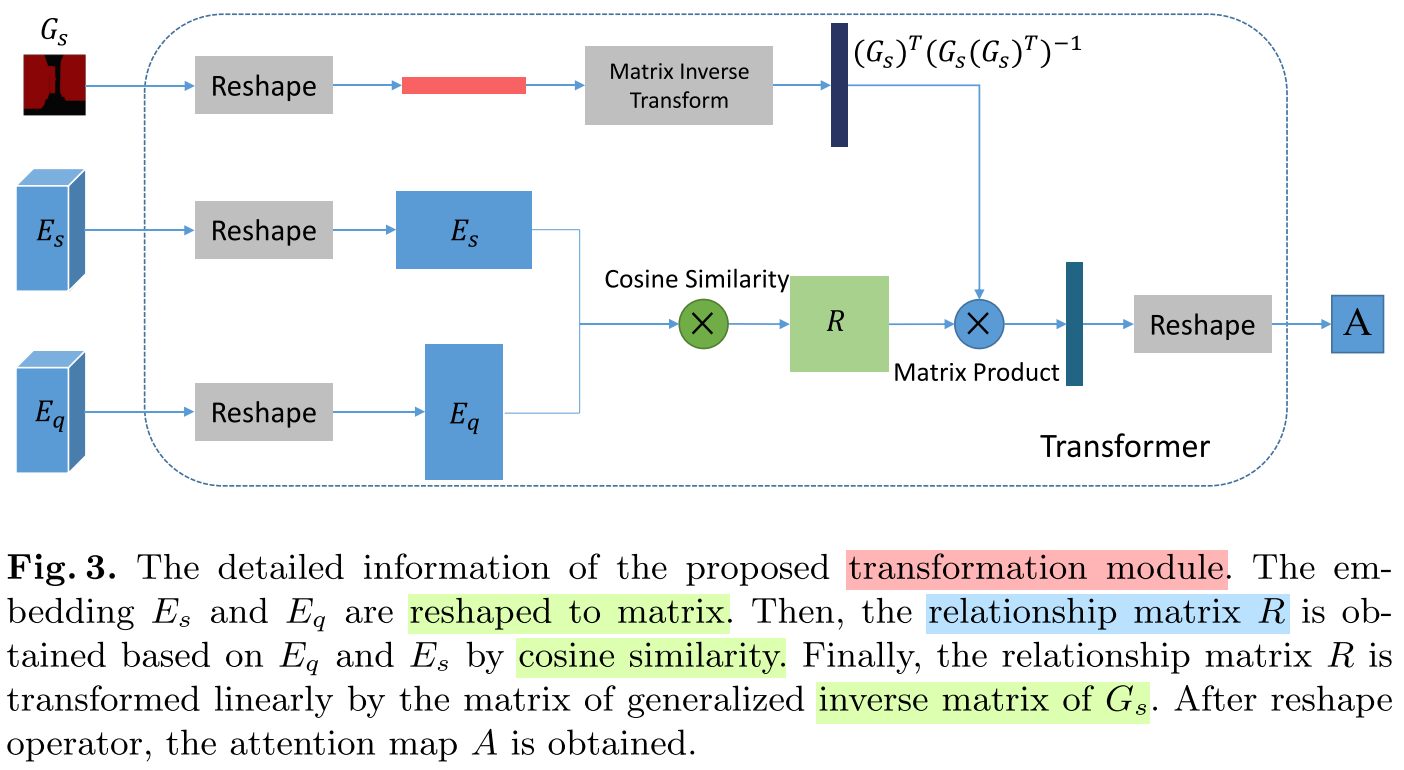
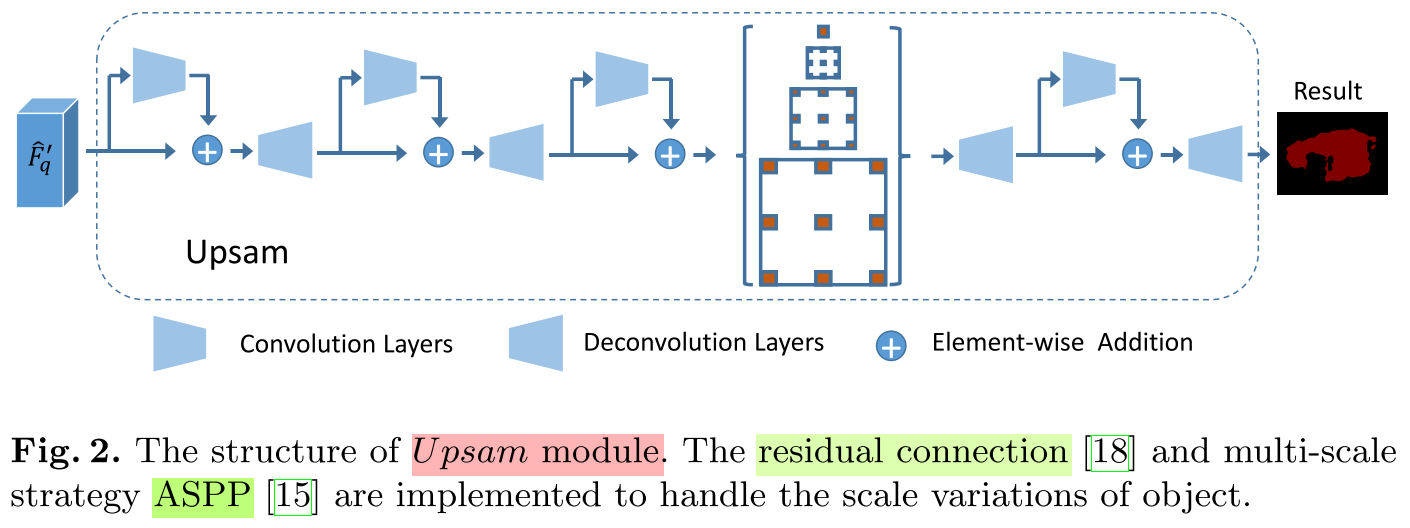
Transformer

$F^\prime_{s}(i,j)=F_{s}(i,j) \times {G_{s}(i,j)}$
$\hat{F^\prime_{q}}(i,j)=\hat{F_{q}}(i,j) \times {A(i,j)}$
$R_{ij}=\frac{\langle E_{si},E_{qj}\rangle}{||E_{si}|| ||E_{qj}||}$
$R_{truth}=G_{q} \cdot G_{s}$
$R=A \cdot G_{s}$
$A=R \cdot [\left( G_{s} \right)^T \left( G_{s} \left( G_{s} \right)^T \right)^{-1}]$
$\hat{A}=\frac{A-\min{(A)}}{\max{(A)}-\min{(A)}}$

Loss function

$L_{m}=\sum_{i}\sum_{j}-(Y(i,j)\log(M(i,j))+(1-Y(i,j))\log(1-M(i,j)))$
$L_{a}=\sum_{i}\sum_{j}-(Y(i,j)\log(M_{a}(i,j))+(1-Y(i,j))\log(1-M_{a}(i,j)))$
$L_{r}=||R-R_{truth}||_2^2$

$L=\lambda_{m}L_{m}+\lambda_{a}L_{a}+\lambda{r}L_{r}$

Experiments

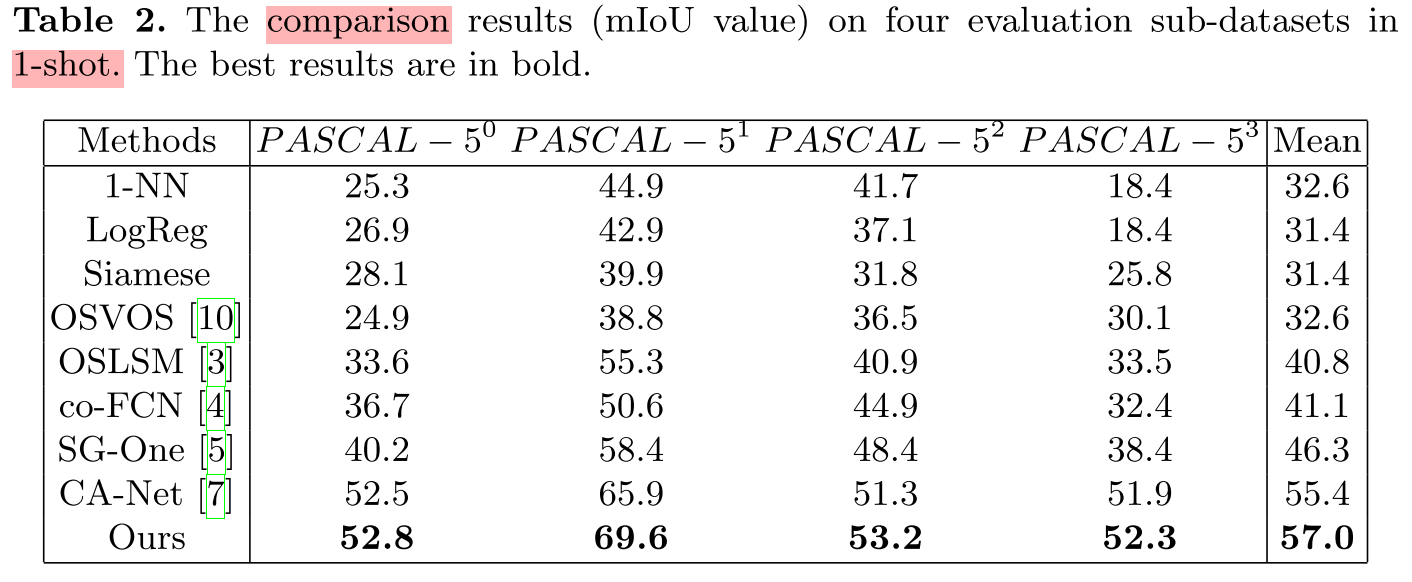
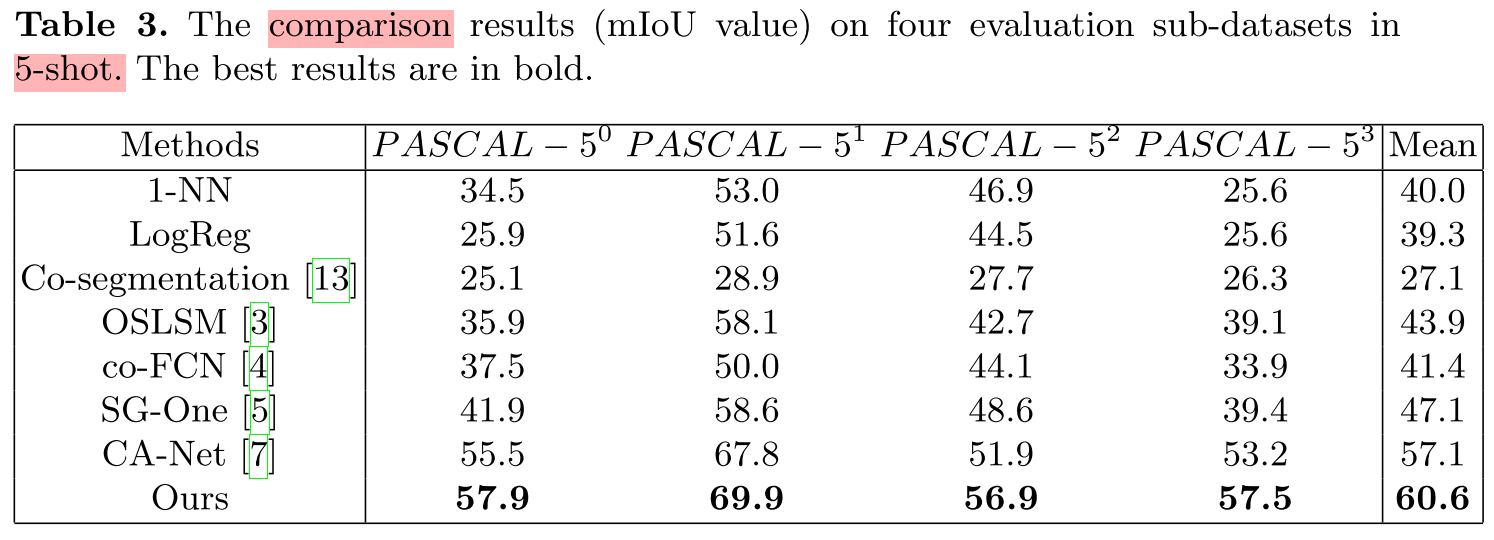
Code

[Updating]

Note

[Updating]

References

[1] Yang Y, Meng F, Li H, et al. A new local transformation module for few-shot segmentation[C]//International Conference on Multimedia Modeling. Springer, Cham, 2020: 76-87.